순환이란?
알고리즘이나 함수가 수행 도중에 자기 자신을 다시 호출하여 문제를 해결하는 기법이다.
순환 알고리즘은 다음과 같은 부분들을 포함한다.
- 순환 호출을 하는 부분
- 순환 호출을 멈추는 부분

만약 순환 호출을 멈추는 부분이 없다면? 시스템 오류가 발생할 때까지 무한정 호출하게 된다.
대부분의 순환은 반복으로 바꾸어 작성할 수 있다.
순환적인 방법이 더 효율적인 예제
숫자 x의 n제곱 값을 구하는 문제: x^n
- 반복
double slow_power(double x, int n)
{
int i;
double result = 1.0;
for(i=0; i<n; i++)
result = result * x;
return(result);
}- 순환
double power(double x, int n)
{
if( n==0 ) return 1;
else if ( (n%2)==0 )
return power(x*x, n/2);
else return x*power(x*x, (n-1)/2);
}
순환 호출을 사용하면 비효율적인 예
피보나치 수열
순환 호출을 사용했을 경우의 비효율성
- 같은 항이 중복해서 계산됨
- 예를 들어 fib(6)을 호출하게 되면 fib(3)이 4번이나 중복되어서 계산됨
- 이러한 현상은 n이 커지면 더 심해짐
히노이탑
문제
- 문제는 막대 A에 쌓여있는 원판 n개를 막대 C로 옮기는 것이다.
- 한 번에 하나의 원판만 이동할 수 있다.
- 맨 위에 있는 원판만 이동할 수 있다.
- 크기가 작은 원판 위에 큰 원판이 쌓일 수 없다.
- 중간의 막대를 임시적으로 이용할 수 있으나 앞의 조건들을 지켜야 한다.
- n=3일 때
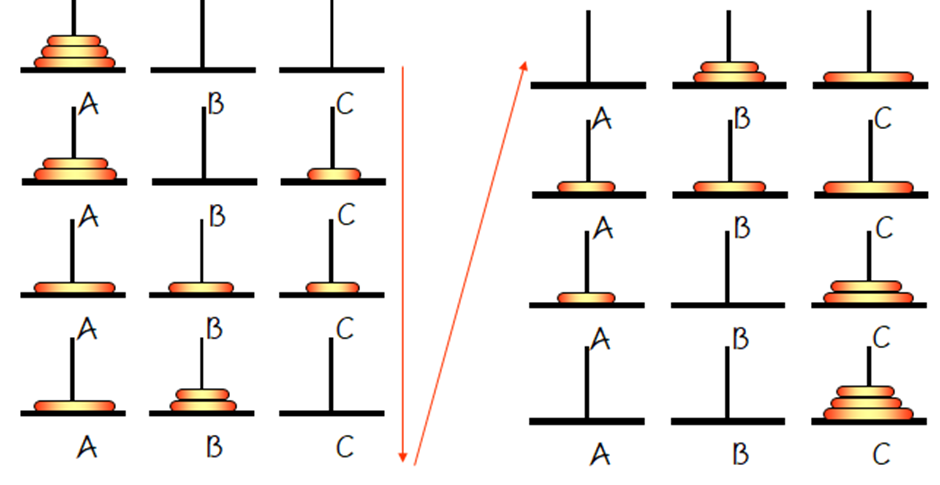
- 일반적인 경우

- n=4일 때
#include <stdio.h>
void hanoi_tower(int n, char from, char tmp, char to)
{
if( n==1 ) printf("원판 1을 %c 에서 %c으로 옮긴다.\n",from,to);
else {
hanoi_tower(n-1, from, to, tmp);
printf("원판 %d을 %c에서 %c으로 옮긴다.\n",n, from, to);
hanoi_tower(n-1, tmp, from, to);
}
}
int main(void)
{
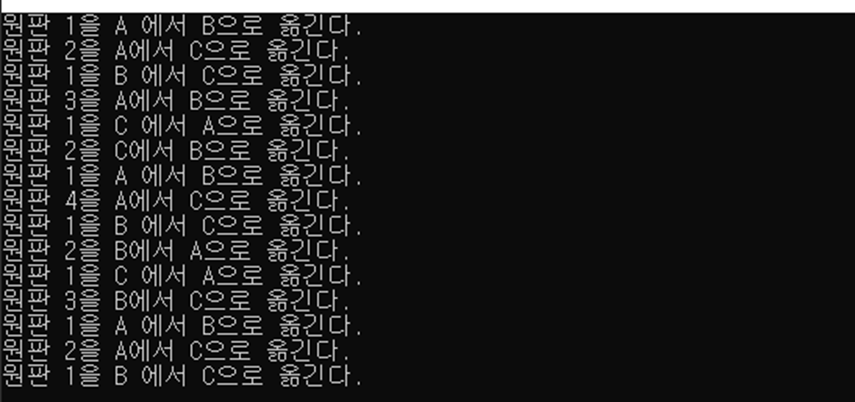
hanoi_tower(4, 'A', 'B', 'C');
retrun 0;
}
히노이탑 시간 복잡도 분석
순환적 알고리즘 방정식: T(n)=2T(n-1)+1 ..……………. ①
귀납적 추론에 의해 다음 방적식이 성립한다.
T(n-1)=2T(n-2)+1 …………….... ②
T(n-2)=2T(n-3)+1 …………….... ③
②식의 T(n-2)에 ③식을 대입하자.
T(n-1)=2(2T(n-3)+1)+1 ……………. ④
① 식의 T(n-1)에 ④식을 대입하자.
T(n)=2(2(2T(n-3)+1)+1)+1
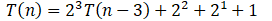
이 식을 일반화시켜보면, 특정숫자 3대신 k로 풀어볼 수 있다.

우리가 알고 있는 수렴조건(기초 단계)인 T(1)=1 를 T(n-k) 에 대입한다면,
n-k=1
k=n-1
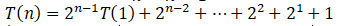
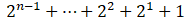
은 G.P.(Geometric Progression) 수열의 합으로써 (2^n)-1이 답이다.
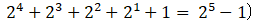
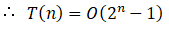
그러므로 우리는 이 알고리즘의 시간복잡도는 O(2^n) 라고 말할 수 있다.
한 예로, 원판갯수 n=5 라면, 총이동 횟수는 2^5-1 = 31번이 걸린다.
'자료구조' 카테고리의 다른 글
| [자료구조] 큐(Queue) (0) | 2022.10.19 |
|---|---|
| [자료구조] 스택(Stack) 예제 (0) | 2022.10.19 |
| [자료구조] 스택(Stack) (0) | 2022.10.19 |
| [자료구조] 배열 구조체 포인터 (0) | 2022.10.18 |
| [자료구조] 자료구조와 알고리즘 (0) | 2022.10.18 |




댓글