※ 18353 병사 배치하기
https://www.acmicpc.net/problem/18353

문제 해결 TIP
최장 증가 부분 수열이란?
예를 들어 다음 수열이 주어졌다고 하자.
3 5 7 9 2 1 4 8
위 수열에서 몇 개의 수를 제거해 부분수열을 만들 수 있다.
3 7 9 1 4 8 (5, 2 제거)
7 9 1 8 (3, 5, 2, 4 제거)
3 5 7 8 (9, 2, 1, 4 제거)
1 4 8 (3, 5, 7, 9, 2 제거)
위와 같이 일부, 혹은 전체가 오름차순인 수열을 '증가 부분 수열'이라고 한다. 그리고 이런 증가 부분 수열 중 가장 긴 수열을 '최장 증가 부분 수열 (LIS)'이라 한다. 즉, 위의 수열의 집합에선 부분수열 3 5 7 8이 LIS이다.
O(N^2) 알고리즘으로 구현할 수 있다. 새로운 배열 dp를 정의하자. 초기 상태는 다음과 같다.

i가 4일 때까지는 수열 A가 오름차순으로 정렬되어 있기 때문에 dp도 1씩 추가해준다.
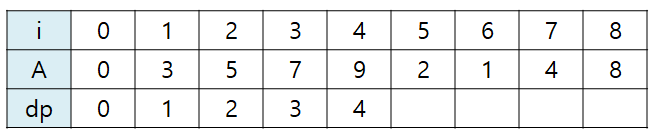
i가 5일 때는 수열 A의 값이 2인데, 이는 i가 0일 때의 값(0)와 1일 때의 값(3) 사이에 위치하므로 dp[5] = 1이다. i가 6일 때는 수열 A의 값이 1이고, 이는 역시 dp[6] = 1이 된다. i가 7일 때는 수열 A의 값이 4이므로 i가 1일 때의 값(3)와 2일 때의 값(5) 사이에 위치한다. 따라서 dp[7] = 2, dp[8] = 4가 된다.

그렇다면 dp의 값들 중 가장 큰 값 4가 수열 A의 LIS 길이가 된다.
위와 같이 진행했을 때 문제의 dp 최종 상태는 다음과 같다.

전체 코드
N = int(input())
A = list(map(int,input().split()))
A.reverse()
#A = [4, 2, 5, 8, 4, 11, 15]
dp = [1] * N
for i in range(1,N):
for j in range(i):
if A[j] < A[i]:
dp[i] = max(dp[i], dp[j]+1)
print(N-max(dp))
#dp = [1, 1, 2, 3, 2, 4, 5]'Python > DP(동적계획법)' 카테고리의 다른 글
| [Algorithm] 삼성 SW 역량테스트 2017 상반기 오전 2번 문제 외주 수익 최대화하기, 코드트리 | 파이썬 (DP, Dynamic Programming) (0) | 2024.08.12 |
|---|---|
| [Algorithm] 백준 1912 연속합 | 파이썬 (DP, Dynamic Programming) (0) | 2024.07.10 |
| [Algorithm] 프로그래머스 정수 삼각형 | 파이썬 (DP, Dynamic Programming) (0) | 2024.07.06 |
| [Algorithm] 이코테 금광 | 파이썬 (DP, Dynamic Programming) (0) | 2024.07.06 |
| [Algorithm] 프로그래머스 멀리 뛰기 | 파이썬 (DP, Dynamic Programming) (0) | 2024.07.05 |




댓글