[문제]
n x m 크기의 금광이 있습니다. 금광은 1 x 1 크기의 칸으로 나누어져 있으며, 각 칸은 특정한 크기의 금이 들어 있습니다. 채굴자는 첫 번째 열부터 출발하여 금을 캐기 시작합니다. 맨 처음에는 첫 번째 열의 어느 행에서든 출발할 수 있습니다. 이후에 m번에 걸쳐서 매번 오른쪽 위, 오른쪽, 오른쪽 아래 3가지 중 하나의 위치로 이동해야 합니다. 결과적으로 채굴자가 얻을 수 있는 금의 최대 크기를 출력하는 프로그램을 작성하세요.
만약 다음과 같이 3 x 4 크기의 금광이 존재한다고 가정합시다.
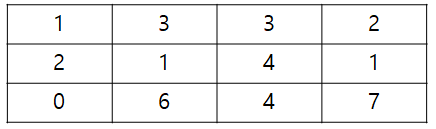
가장 왼쪽 위의 위치를 (1, 1), 가장 오른쪽 아래의 위치를 (n, m)이라고 할 때, 위 예시에서는 (2, 1) → (3, 2) → (3, 3) → (3, 4)의 위치로 이동하면 총 19만큼의 금을 채굴할 수 있으며, 이때의 값이 최댓값입니다.
[입력 조건]
- 첫째 줄에 테스트 케이스 T가 입력됩니다. (1<=T<=1000)
- 매 테스트케이스 첫째 줄에 n과 m이 공백으로 구분되어 입력됩니다. (1<=n, m<= 20) 둘째 줄에 n x m개의 위치에 매장된 금의 개수가 공백으로 구분되어 입력됩니다. (0<=각 위치에 매장된 금의 개수 <= 100)
[출력 조건]
- 테스트 케이스마다 채굴자가 얻을 수 있는 금의 최대 크기를 출력합니다. 각 테스트 케이스는 줄 바꿈을 이용해 구분합니다.
[입력 예시]
2
3 4
1 3 3 2 2 1 4 1 0 6 4 7
4 4
1 3 1 5 2 2 4 1 5 0 2 3 0 6 1 2
[출력 예시]
19
16
문제 해결 TIP
문제에 따라 금광의 모든 위치에 대하여, 1) 왼쪽 위에서 오는 경우 2) 왼쪽 아래에서 오는 경우 3) 왼쪽에서 오는 경우의 3가지 경우가 존재한다. 따라서 이 3가지 경우 중 가장 많은 금을 가지고 있는 경우를 테이블에 저장해주면 된다.
dp테이블은 다음과 같이 바뀌게 된다.
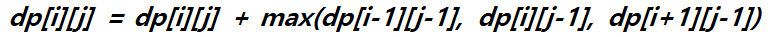

전체 코드
T = int(input())
for i in range(T):
graph = []
n, m = map(int,input().split())
graph =list(map(int,input().split()))
#graph = [[1, 3, 3, 2, 2, 1, 4, 1, 0, 6, 4, 7]]
dp = [[0]*m for _ in range(n)]
#2차원 배열 형태로 바꾸기(dp 초기화)
for i in range(n):
for j in range(m):
dp[i][j] = graph[i*m+j]
#dp = [[1, 3, 3, 2], [2, 1, 4, 1], [0, 6, 4, 7]]
for j in range(1,m):
for i in range(n):
#왼쪽 위에서 오는 경우
if i == 0:
left_up = 0
else:
left_up = dp[i-1][j-1]
#왼쪽 아래에서 오는 경우
if i == n-1:
left_down = 0
else:
left_down = dp[i+1][j-1]
#왼쪽에서 오는 경우
left = dp[i][j-1]
dp[i][j] = dp[i][j] + max(left_up, left_down, left)
result = 0
for i in range(n):
result = max(result,dp[i][m-1])
print(result)'Python > DP(동적계획법)' 카테고리의 다른 글
| [Algorithm] 백준 18353, 이코테 병사 배치하기, 최장 증가 부분 수열 | 파이썬 (DP, Dynamic Programming) (0) | 2024.07.07 |
|---|---|
| [Algorithm] 프로그래머스 정수 삼각형 | 파이썬 (DP, Dynamic Programming) (0) | 2024.07.06 |
| [Algorithm] 프로그래머스 멀리 뛰기 | 파이썬 (DP, Dynamic Programming) (0) | 2024.07.05 |
| [Algorithm] 이코테 개미 전사 | 파이썬 (DP, Dynamic Programming) (0) | 2024.07.03 |
| [Algorithm] 백준 1463, 이코테 1로 만들기 | 파이썬 (DP, Dynamic Programming) (0) | 2024.07.03 |




댓글